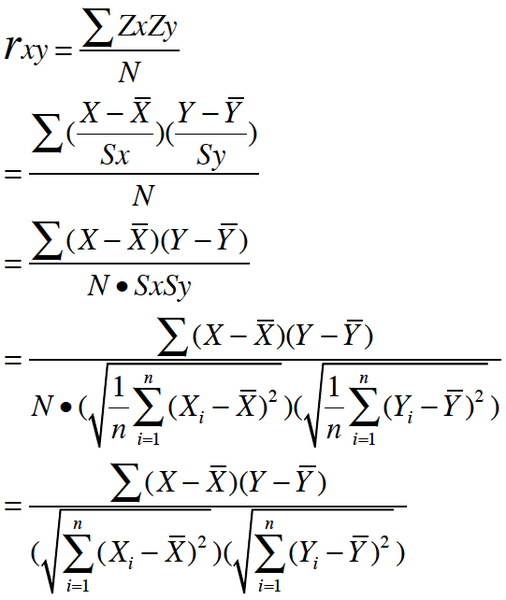|
皮尔逊相关系数理解有两个角度
其一, 按照高中数学水平来理解, 它很简单, 可以看做将两组数据首先做Z分数处理之后, 然后两组数据的乘积和除以样本数 Z分数一般代表正态分布中, 数据偏离中心点的距离.等于变量减掉平均数再除以标准差.(就是高考的标准分类似的处理) 标准差则等于变量减掉平均数的平方和,再除以样本数,最后再开方. 所以, 根据这个最朴素的理解,我们可以将公式依次精简为:
其二, 按照大学的线性数学水平来理解, 它比较复杂一点,可以看做是两组数据的向量夹角的余弦. 皮尔逊相关的约束条件从以上解释, 也可以理解皮尔逊相关的约束条件:
在实践统计中,一般只输出两个系数,一个是相关系数,也就是计算出来的相关系数大小,在-1到1之间;另一个是独立样本检验系数,用来检验样本一致性. 先举个手算的例子使用维基中的例子: 例如,假设五个国家的国民生产总值分别是1、2、3、5、8(单位10亿美元),又假设这五个国家的贫困比例分别是11%、12%、13%、15%、18%。创建2个向量.(R语言) x<-c(1,2,3,5,8)y<-c(0.11,0.12,0.13,0.15,0.18)按照维基的例子,应计算出相关系数为1出来.我们看看如何一步一步计算出来的.
x的平均数是:3.8 用大白话来写就是:
(1-3.8)*(0.11-0.138)=0.0784 0.0784+0.0324+0.0064+0.0144+0.1764=0.308 同理, 分号下面的,分别是:
sum((x-mean(x))^2)=30.8 用大白话来写,分别是:
(1-3.8)^2=7.84 #平方 7.84+3.24+0.64+1.44+17.64=30.8 同理,求得: sum((y-mean(y))^2)= 0.00308然后再开平方根,分别是:
30.8^0.5=5.549775 用分子除以分母,就计算出最终结果: 0.308/(5.549775*0.05549775)=1
假设这两组都是正态分布.我们来求这两者的皮尔逊相关系数,R脚本如下: > x<-rnorm(n=100,mean=35,sd=5) #创建一组平均数为35,标准差为5,样本数为100的随机数 > y<-rnorm(n=100,mean=45,sd=8) #创建一组平均数为45,标准差为8,样本数为100的随机数 > cor.test(x,y,method="pearson") #计算这两组数的相关,并进行T检验然后R输出结果为: Pearson's product-moment correlation data: x and y t = -0.0269, df = 98, p-value = 0.9786 alternative hypothesis: true correlation is not equal to 0 95 percent confidence interval: -0.1990316 0.1938019 sample estimates: cor -0.002719791当然,这里是随机数.也可以用非随机的验证一下计算. 皮尔逊相关系数用于网站开发直接将R与Ruby关联起来 调用很简单,仿照上述例子: cor(x,y)就输出系数结果了. 有这么几个库可以参考: https://github.com/alexgutteridge/rsr... https://github.com/davidrichards/stat... https://github.com/jtprince/simpler 说明, 以上为ruby调用库. pythone程序员可以参考: Rpy ()
(责任编辑:laiquliu) |